The flux of a vector field \(\vec{F}\) through
a surface, \(S\), parametrized by \(\vec R(u,v)\) is
\[
\iint_S \vec{F}\cdot\vec{dS}
=\iint_S \vec{F}(\vec R(u,v))\cdot\vec{N}\,du\,dv
\]
Note that notation \(\vec{F}(\vec R(u,v))\) means the vector field
\(\vec{F}\) must be evaluated on the surface.
Flux is often used in subjects such as electromagnetism and fluid dynamics.
Electric fields, magnetic fields, and fluid flows can be expressed as vector
fields, and it is often useful to know how much of one of these fields is
flowing through a surface.
The expansion of a vector field \(\vec{F}\)
is the flux of the vector field outward through
a closed surface (for example, a sphere, box, or a cylinder
with the ends closed). The contraction of
a vector field \(\vec{F}\) is the negative of the
expansion.
See a
previous page for a discussion of the orientation of the surface.
So to say the flux is outward means the normal
is pointing outward.
Find the flux of the velocity field,
\(\vec{V}=\left\langle 2xz,2yz,x^2+y^2\right\rangle\), through
the paraboloid, \(P\), given by \(z=x^2+y^2\) for \(z \le 4\) with the
normal pointing down and out.
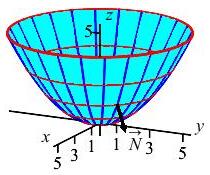
The flux is \(\displaystyle \iint_P \vec{V}\cdot\,d\vec{S}\).
To find a parametrization, we start with cylindrical coordinates:
\[
\vec R(r,\theta,z)=\left\langle r\cos\theta,r\sin\theta,z\right\rangle
\]
and substitute \(z=x^2+y^2=r^2\). This reduces the expression to two parameters:
\[
\vec R(r,\theta)=\left\langle r\cos\theta,r\sin\theta,r^2\right\rangle
\]
Now we find the tangent vectors and the normal:
\[
\begin{array}{r}
\\
\vec{e}_r= \\
\vec{e}_\theta=
\end{array}
\left|
\begin{array}{ccc}
\hat{\imath} & \hat{\jmath} & \hat{k} \\
\cos\theta & \sin\theta & 2r \\
-r\sin\theta & r\cos\theta & 0
\end{array}
\right|
=\vec{e}_r\times\vec{e}_\theta=\vec{N}
\]
So
\[\begin{aligned}
\vec{N}
&=\hat{\imath}(-2r^2\cos\theta)
-\hat{\jmath}(--2r^2\sin\theta)
+\hat{k}(r\cos^2\theta--r\sin^2\theta) \\
&=\left\langle -2r^2\cos\theta,-2r^2\sin\theta,r\right\rangle
\end{aligned}\]
The problem defines the normal to be down and out. However,\(r \ge 0\) so that the
\(z\)-component of \(\vec N\) is positive, which is up. Further, in the first quadrant,
\(\sin\theta \ge 0\) and \(\cos\theta \ge 0\) so that the \(x\)- and
\(y\)-components of \(\vec N\) are negative or inward. So we need to reverse
\(\vec{N}\).
\[
\text{Reverse:}\qquad\vec{N}
=\left\langle 2r^2\cos\theta,2r^2\sin\theta,-r\right\rangle
\]
Next, we evaluate the vector field on the surface:
\[
\left.\vec{V}\right|_{\vec R(r,\theta)}
=\left\langle 2r^3\cos\theta,2r^3\sin\theta,r^2\right\rangle
\]
and compute its dot product with the normal:
\[\begin{aligned}
\vec{V}\cdot\vec{N}
&=\left\langle 2r^3\cos\theta,2r^3\sin\theta,r^2\right\rangle\cdot
\left\langle 2r^2\cos\theta,2r^2\sin\theta,-r\right\rangle \\
&=4r^5-r^3
\end{aligned}\]
Our integral is
\[\begin{aligned}
\text{Flux}
&=\int \int \vec{V}\cdot\vec{N}\,dr\,d\theta
=\int_0^{2\pi}\int_0^2 (4r^5-r^3)\,dr\,d\theta \\
&=2\pi\left[\dfrac{2r^6}{3}-\dfrac{r^4}{4}\right]_0^2
=2\pi\left(\dfrac{128-12}{3}\right)
=\dfrac{232}{3}\pi
\end{aligned}\]
Caution:
Do not put an extra factor of \(r\) into the integrand, just because you see
a \(dr\,d\theta\). This \(r\) is already in \(\vec{N}\). While these
variables are similar to those used in cylindrical coordinates, they are
not the same. Here, \(r\) and \(\theta\) are parameters for the
surface, not cylindrical (nor polar) coordinates.
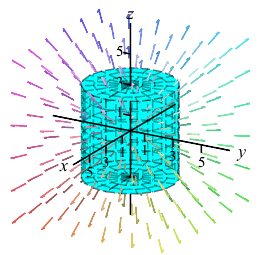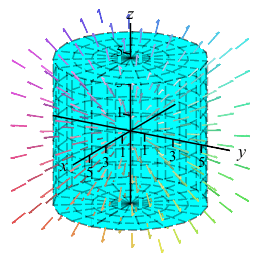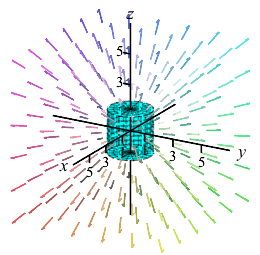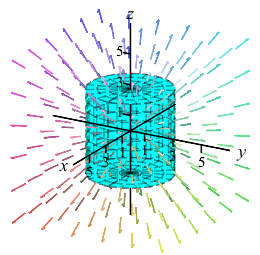
The electric field of a positive point charge is given by:
\[\begin{aligned}
\vec E&(x,y,z)=\dfrac{\hat r}{r^2}=\dfrac{\vec r}{r^3} \\
&=\left\langle \dfrac{x}{\left(x^2+y^2+z^2\right)^{3/2}},
\dfrac{y}{\left(x^2+y^2+z^2\right)^{3/2}},
\dfrac{z}{\left(x^2+y^2+z^2\right)^{3/2}}\right\rangle
\end{aligned}\]
Find the expansion of the electric field out of the cylinder, \(C\),
given by \(x^2+y^2 \le 9\) and \(-3 \le z \le 3\).
There are \(3\) pieces to the boundary: the curved sides, \(S\), the
top, \(T\), and the bottom, \(B\). Compute the flux through each and
add them up. To parametrize each surface, start with cylindrical
coordinates and set \(r=3\) for the sides, \(z=3\) for the top and
\(z=-3\) for the bottom.
There are \(3\) pieces to the boundary: the curved sides, \(S\), the
top, \(T\), and the bottom, \(B\). We will compute the flux through
each and add them up.
To parametrize the curved side surface, we start with cylindrical
coordinates:
\[
\vec R(r,\theta,z)
=\left\langle r\cos\theta,r\sin\theta,z\right\rangle
\]
and set \(r=3\):
\[
\vec R(\theta,z)
=\left\langle 3\cos\theta,3\sin\theta,z\right\rangle
\]
The tangent and normal vectors are:
\[\begin{aligned}
\vec e_\theta&=\left\langle -3\sin\theta,3\cos\theta,0\right\rangle \\
\vec e_z&=\left\langle 0,0,1\right\rangle \\
\vec N&=\left\langle 3\cos\theta,3\sin\theta,0\right\rangle
\end{aligned}\]
As should be expected, the normal is horizontal and the \(x\) and \(y\)
components are parallel to those for the position vector. Like the
position vector, the normal points outward, as required.
On the surface, the electric field becomes:
\[
\vec E(\theta,z)
=\left\langle \dfrac{3\cos\theta}{\left(9+z^2\right)^{3/2}},
\dfrac{3\sin\theta}{\left(9+z^2\right)^{3/2}},
\dfrac{z}{\left(9+z^2\right)^{3/2}}\right\rangle
\]
and its dot product with the normal is:
\[
\vec E\cdot\vec N
=\dfrac{9\cos^2\theta}{\left(9+z^2\right)^{3/2}}
+\dfrac{9\sin^2\theta}{\left(9+z^2\right)^{3/2}}
=\dfrac{9}{\left(9+z^2\right)^{3/2}}
\]
So the flux is:
\[\begin{aligned}
\text{Flux}_S
&=\iint_S \vec E\cdot d\vec S
=\iint_S \vec E\cdot \vec N\,d\theta\,dz \\
&=\int_{-3}^3\int_0^{2\pi} \dfrac{9}{\left(9+z^2\right)^{3/2}}\,d\theta\,dz
=2\pi\int_{-3}^3 \dfrac{9}{\left(9+z^2\right)^{3/2}}\,dz
\end{aligned}\]
At this point we use the trig substitution \(z=3\tan\alpha\) and
\(dz=3\sec^2\alpha\,d\alpha\):
\[\begin{aligned}
\text{Flux}_S
&=2\pi\int_{z=-3}^{3}
\dfrac{9}{\left(9+9\tan^2\alpha\right)^{3/2}}3\sec^2\alpha\,d\alpha \\
&=2\pi\int_{z=-3}^{3}
\dfrac{1}{\left(1+\tan^2\alpha\right)^{3/2}}\sec^2\alpha\,d\alpha \\
&=2\pi\int_{z=-3}^{3} \cos\alpha\,d\alpha
=2\pi\left[\sin\alpha\dfrac{}{}\right]_{z=-3}^{3}
\end{aligned}\]
We now draw a right triangle with angle \(\alpha\), opposite side \(z\),
adjacent side \(3\) and hypotenuse \(\sqrt{9+z^2}\). Then
\(\sin\alpha=\dfrac{z}{\sqrt{9+z^2}}\). So
\[\begin{aligned}
\text{Flux}_S
&=2\pi\left[\dfrac{z}{\sqrt{9+z^2}}\right]_{z=-3}^{3}
=4\pi\dfrac{3}{\sqrt{18}}
=2\pi\sqrt{2}
\end{aligned}\]
To parametrize the top surface, we start with cylindrical
coordinates and set \(z=3\):
\[
\vec R(r,\theta)
=\left\langle r\cos\theta,r\sin\theta,3\right\rangle
\]
After finding the tangent vectors, the normal vector is
\(\vec N=\left\langle 0,0,r\right\rangle\).
Since the \(z\) component is positive, this points up as required.
On the surface, the electric field becomes:
\[
\vec E(\theta,z)
=\left\langle \dfrac{r\cos\theta}{\left(r^2+9\right)^{3/2}},
\dfrac{r\sin\theta}{\left(r^2+9\right)^{3/2}},
\dfrac{3}{\left(r^2+9\right)^{3/2}}\right\rangle
\]
and its dot product with the normal is:
\[
\vec E\cdot\vec N
=\dfrac{3r}{\left(r^2+9\right)^{3/2}}
\]
So the flux is:
\[\begin{aligned}
\text{Flux}_T
&=\iint_T \vec E\cdot d\vec S
=\iint_T \vec E\cdot \vec N\,dr\,d\theta \\
&=\int_0^{2\pi}\int_0^3 \dfrac{3r}{\left(r^2+9\right)^{3/2}}\,dr\,d\theta
=2\pi\int_0^3 \dfrac{3r}{\left(r^2+9\right)^{3/2}}\,dr
\end{aligned}\]
At this point we use the substitution \(u=r^2+9\) and
\(du=2r\,dr\):
\[\begin{aligned}
\text{Flux}_T
&=\pi\int_{r=0}^3 \dfrac{3}{u^{3/2}}\,du
=\pi\left[-2\dfrac{3}{u^{1/2}}\right]_{r=0}^3
=-2\pi\left[\dfrac{3}{\left(r^2+9\right)^{1/2}}\right]_0^3 \\
&=-\dfrac{2\pi 3}{\left(18\right)^{1/2}}
+\dfrac{2\pi 3}{\left(9\right)^{1/2}}
=2\pi-\pi\sqrt{2}
\end{aligned}\]
To parametrize the bottom surface, we start with cylindrical
coordinates and set \(z=-3\):
\[
\vec R(r,\theta)
=\left\langle r\cos\theta,r\sin\theta,-3\right\rangle
\]
After finding the tangent vectors, the normal vector is
\(\vec N=\left\langle 0,0,r\right\rangle\).
Since the \(z\) component is positive, this points up but we need
it to point down to be out from the solid cylinder. So we reverse
it:
\[
\text{Reverse:}\qquad\vec N
=\left\langle 0,0,-r\right\rangle
\]
On the surface, the electric field becomes:
\[
\vec E(\theta,z)
=\left\langle \dfrac{r\cos\theta}{\left(r^2+9\right)^{3/2}},
\dfrac{r\sin\theta}{\left(r^2+9\right)^{3/2}},
\dfrac{-3}{\left(r^2+9\right)^{3/2}}\right\rangle
\]
and its dot product with the normal is (again):
\[
\vec E\cdot\vec N
=\dfrac{3r}{\left(r^2+9\right)^{3/2}}
\]
So the flux is (again):
\[\begin{aligned}
\text{Flux}_B
&=\iint_B \vec E\cdot d\vec S
=\iint_B \vec E\cdot \vec N\,dr\,d\theta \\
&=\int_0^{2\pi}\int_0^3 \dfrac{3r}{\left(r^2+9\right)^{3/2}}\,dr\,d\theta \\
&=\cdots=2\pi-\pi\sqrt{2}
\end{aligned}\]
Finally, we add up the flux through the \(3\) surfaces to get the
expansion out of the cylinder:
\[\begin{aligned}
\text{Expansion}&=\iint_C \vec E\cdot d\vec S
=\text{Flux}_S+\text{Flux}_T+\text{Flux}_B \\
&=\iint_S \vec E\cdot d\vec S+\iint_T \vec E\cdot d\vec S
+\iint_B \vec E\cdot d\vec S \\
&=2\pi\sqrt{2}
+2\pi-\pi\sqrt{2}
+2\pi-\pi\sqrt{2}
=4\pi
\end{aligned}\]
Find the expansion of the electric field out of the cylinder, \(C\),
given by \(x^2+y^2 \le R^2\) and \(-H \le z \le H\).
There are \(3\) pieces to the boundary: the curved sides, \(S\), the
top, \(T\), and the bottom, \(B\). We will compute the flux through
each and add them up.
To parametrize the curved side surface, we start with cylindrical
coordinates:
\[
\vec R(r,\theta,z)
=\left\langle r\cos\theta,r\sin\theta,z\right\rangle
\]
and set \(r=R\):
\[
\vec R(\theta,z)
=\left\langle R\cos\theta,R\sin\theta,z\right\rangle
\]
The tangent and normal vectors are:
\[\begin{aligned}
\vec e_\theta&=\left\langle -R\sin\theta,R\cos\theta,0\right\rangle \\
\vec e_z&=\left\langle 0,0,1\right\rangle \\
\vec N&=\left\langle R\cos\theta,R\sin\theta,0\right\rangle
\end{aligned}\]
As should be expected, the normal is horizontal and the \(x\) and \(y\)
components are parallel to those for the position vector. Like the
position vector, the normal points outward, as required.
On the surface, the electric field becomes:
\[
\vec E(\theta,z)
=\left\langle \dfrac{R\cos\theta}{\left(R^2+z^2\right)^{3/2}},
\dfrac{R\sin\theta}{\left(R^2+z^2\right)^{3/2}},
\dfrac{z}{\left(R^2+z^2\right)^{3/2}}\right\rangle
\]
and its dot product with the normal is:
\[
\vec E\cdot\vec N
=\dfrac{R^2\cos^2\theta}{\left(R^2+z^2\right)^{3/2}}
+\dfrac{R^2\sin^2\theta}{\left(R^2+z^2\right)^{3/2}}
=\dfrac{R^2}{\left(R^2+z^2\right)^{3/2}}
\]
So the flux is:
\[\begin{aligned}
\text{Flux}_S
&=\iint_S \vec E\cdot d\vec S
=\iint_S \vec E\cdot \vec N\,d\theta\,dz \\
&=\int_{-H}^H\int_0^{2\pi} \dfrac{R^2}{\left(R^2+z^2\right)^{3/2}}\,d\theta\,dz
=2\pi\int_{-H}^H \dfrac{R^2}{\left(R^2+z^2\right)^{3/2}}\,dz
\end{aligned}\]
At this point we use the trig substitution \(z=R\tan\alpha\) and
\(dz=R\sec^2\alpha\,d\alpha\):
\[\begin{aligned}
\text{Flux}_S
&=2\pi\int_{z=-H}^{H}
\dfrac{R^2}{\left(R^2+R^2\tan^2\alpha\right)^{3/2}}R\sec^2\alpha\,d\alpha \\
&=2\pi\int_{z=-H}^{H}
\dfrac{1}{\left(1+\tan^2\alpha\right)^{3/2}}\sec^2\alpha\,d\alpha \\
&=2\pi\int_{z=-H}^{H} \cos\alpha\,d\alpha
=2\pi\left[\sin\alpha\dfrac{}{}\right]_{z=-H}^{H}
\end{aligned}\]
We now draw a right triangle with angle \(\alpha\), opposite side \(z\),
adjacent side \(R\) and hypotenuse \(\sqrt{R^2+z^2}\). Then
\(\sin\alpha=\dfrac{z}{\sqrt{R^2+z^2}}\). So
\[\begin{aligned}
\text{Flux}_S
&=2\pi\left[\dfrac{z}{\sqrt{R^2+z^2}}\right]_{z=-H}^{H}
=\dfrac{4\pi H}{\sqrt{R^2+H^2}}
\end{aligned}\]
To parametrize the top surface, we start with cylindrical
coordinates and set \(z=H\):
\[
\vec R(r,\theta)
=\left\langle r\cos\theta,r\sin\theta,H\right\rangle
\]
After finding the tangent vectors, the normal vector is
\(\vec N=\left\langle 0,0,r\right\rangle\).
Since the \(z\) component is positive, this points up as required.
On the surface, the electric field becomes:
\[
\vec E(\theta,z)
=\left\langle \dfrac{r\cos\theta}{\left(r^2+H^2\right)^{3/2}},
\dfrac{r\sin\theta}{\left(r^2+H^2\right)^{3/2}},
\dfrac{H}{\left(r^2+H^2\right)^{3/2}}\right\rangle
\]
and its dot product with the normal is:
\[
\vec E\cdot\vec N
=\dfrac{Hr}{\left(r^2+H^2\right)^{3/2}}
\]
So the flux is:
\[\begin{aligned}
\text{Flux}_T
&=\iint_T \vec E\cdot d\vec S
=\iint_T \vec E\cdot \vec N\,dr\,d\theta \\
&=\int_0^{2\pi}\int_0^R \dfrac{Hr}{\left(r^2+H^2\right)^{3/2}}\,dr\,d\theta
=2\pi\int_0^R \dfrac{Hr}{\left(r^2+H^2\right)^{3/2}}\,dr
\end{aligned}\]
At this point we use the substitution \(u=r^2+H^2\) and
\(du=2r\,dr\):
\[\begin{aligned}
\text{Flux}_T
&=\pi\int_{r=0}^R \dfrac{H}{u^{3/2}}\,du
=\pi\left[-2\dfrac{H}{u^{1/2}}\right]_{r=0}^R
=-2\pi\left[\dfrac{H}{\left(r^2+H^2\right)^{1/2}}\right]_0^R \\
&=-\dfrac{2\pi H}{\left(R^2+H^2\right)^{1/2}}
+\dfrac{2\pi H}{\left(H^2\right)^{1/2}}
=2\pi-\dfrac{2\pi H}{\left(R^2+H^2\right)^{1/2}}
\end{aligned}\]
To parametrize the bottom surface, we start with cylindrical
coordinates and set \(z=-H\):
\[
\vec R(r,\theta)
=\left\langle r\cos\theta,r\sin\theta,-H\right\rangle
\]
After finding the tangent vectors, the normal vector is
\(\vec N=\left\langle 0,0,r\right\rangle\).
Since the \(z\) component is positive, this points up but we need
it to point down to be out from the solid cylinder. So we reverse
it:
\[
\text{Reverse:}\qquad\vec N
=\left\langle 0,0,-r\right\rangle
\]
On the surface, the electric field becomes:
\[
\vec E(\theta,z)
=\left\langle \dfrac{r\cos\theta}{\left(r^2+H^2\right)^{3/2}},
\dfrac{r\sin\theta}{\left(r^2+H^2\right)^{3/2}},
\dfrac{-H}{\left(r^2+H^2\right)^{3/2}}\right\rangle
\]
and its dot product with the normal is (again):
\[
\vec E\cdot\vec N
=\dfrac{Hr}{\left(r^2+H^2\right)^{3/2}}
\]
So the flux is (again):
\[\begin{aligned}
\text{Flux}_B
&=\iint_B \vec E\cdot d\vec S
=\iint_B \vec E\cdot \vec N\,dr\,d\theta \\
&=\int_0^{2\pi}\int_0^R \dfrac{Hr}{\left(r^2+H^2\right)^{3/2}}\,dr\,d\theta \\
&=\cdots=2\pi-\dfrac{2\pi H}{\left(R^2+H^2\right)^{1/2}}
\end{aligned}\]
Finally, we add up the flux through the \(3\) surfaces to get the
expansion out of the cylinder:
\[\begin{aligned}
\text{Expansion}&=\iint_C \vec E\cdot d\vec S
=\text{Flux}_S+\text{Flux}_T+\text{Flux}_B \\
&=\iint_S \vec E\cdot d\vec S+\iint_T \vec E\cdot d\vec S
+\iint_B \vec E\cdot d\vec S \\
&=\dfrac{4\pi H}{\sqrt{R^2+H^2}}
+2\pi-\dfrac{2\pi H}{\left(R^2+H^2\right)^{1/2}}
+2\pi-\dfrac{2\pi H}{\left(R^2+H^2\right)^{1/2}} \\
&=4\pi
\end{aligned}\]
Compare the expansion for various values of \(R\) and \(H\).
Does the expansion get larger or smaller as \(R\) or \(H\) gets
bigger.
The expansion is independent of \(R\) and \(H\).
The expansion,
\(\displaystyle \iint_C \vec E\cdot d\vec S=4\pi\),
independent of \(R\) and \(H\).
In a
later chapter, we will learn that Gauss' Theorem says
this integral is surface independent. Consequently, changing the
values of \(R\) and \(H\) does not change the value of the integral.
Placeholder text:
Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum
Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum
Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum
Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum
Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum